Prueba Diagnóstica de Matemática 3° grado de secundaria con respuestas

Esta prueba contiene 28 preguntas: 23 de opción múltiple, 4 de respuesta abierta extensa (RAE) y 1 de respuesta abierta corta (RAC). Las respuestas de los estudiantes permitirán conocer el estado de sus aprendizajes en el momento actual.

Resuelve problemas de cantidad.

01.- Un médico le prescribió a Sergio una pastilla diaria para controlar su presión arterial. La siguiente imagen muestra el empaque de pastillas que Sergio adquirió.

Luego de unos días de tomar responsablemente sus pastillas, Sergio se ha dado cuenta de que ya ha tomado más de ½ del total de pastillas del empaque, pero menos de 2/3. ¿Cuántos días lleva Sergio tomando sus pastillas?

a) 4 días.

b) 6 días.

c) 7 días.

d) 8 días.

02.- Jorge coloca cubiertos (cucharas y tenedores) en una mesa vacía. Luego, afirma lo siguiente:

“La cantidad de cucharas es 2/3 del total de cubiertos de la mesa”.

¿Cuál de los siguientes conjuntos de cubiertos representa lo señalado por Jorge?

Respuesta d)

03.- Un país tiene aproximadamente 32 millones de habitantes. Las ¾ partes de esta población utilizan las redes sociales para comunicarse.

Según esta información, aproximadamente, ¿cuántos habitantes de este país utilizan las redes sociales para comunicarse?

a) 27 millones de habitantes.

b) 24 millones de habitantes.

c) 11 millones de habitantes.

d) 8 millones de habitantes.

04.- Lee la siguiente noticia.

Solo 4 % de los hogares rurales tiene internet.

Así lo indica la medición del Instituto Nacional de Estadística e Informática del Perú (INEI) correspondiente al primer trimestre del 2019.

Según esta noticia, ¿cuál es la alternativa que representa la información mostrada?

a) Por cada 10 hogares rurales que hay en el Perú, 4 tienen internet.

b) 4 de cada 100 hogares rurales del Perú tienen internet.

c) La cuarta parte de los hogares rurales en el Perú tiene internet.

d) 1 de cada 4 hogares rurales del Perú tiene internet.

05.- Las orcas son mamíferos marinos. Se las conoce como “ballenas asesinas” debido a su gran tamaño y a su capacidad de cazar ballenas, focas o leones marinos.

En la siguiente imagen, se muestra la longitud de una orca hembra.

¿Cuál de las siguientes expresiones representa la longitud de esta orca hembra?

a) 8 ½ m

b) 8 2/5 m

c) 8 ¼ m

d) 8 5/2 m

06.- Una tienda de ropa ofrece un descuento del 20 % en casacas. Además, ofrece un descuento adicional del 10 % si la compra se realiza al contado.

Al saber de esta oferta, Beto afirma lo siguiente:

“Me conviene comprar una casaca, ya que, si pago al contado, el descuento total será del 30 %”.

¿Estás de acuerdo con la afirmación de Beto?

Sí No (Marca tu respuesta con una X)

¿Por qué? Justifica tu respuesta mediante un ejemplo.

Justifica aquí tu respuesta.

Respuesta adecuada

El estudiante manifiesta de forma explícita o implícita su desacuerdo con la afirmación de Beto. En su respuesta, evidencia la comprensión que tiene sobre los descuentos sucesivos (expresados en porcentajes) que se aplican al comprar una casaca al contado. Puede utilizar representaciones numéricas, gráficas o verbales para justificar su respuesta. Por ejemplo:

• No estoy de acuerdo, porque:

- Primer descuento: 20 %x

- Segundo descuento: 10 %(80%x) = 8 %x

- Descuento total: 20 %x + 8 %x = 28 %x

• El descuento total solo equivale al 28 % del precio original y es menor que 30 % del precio original.

• Sea el precio de la ropa 100 soles. El descuento del 20 % representa 0,20 de 100, por lo que el descuento es 20 soles. Por lo tanto, se pagarían 80 soles por la ropa. Luego, dado que hay un descuento adicional del 10 %, este equivale a 0,10 de 80 (precio con el primer descuento ya aplicado). Eso nos da 8 soles de descuento, así que solo se pagarían 72 soles. Al final, solo se descontaron 28 soles y no 30 soles, que es el 30 % de 100.

• No es correcto, porque:

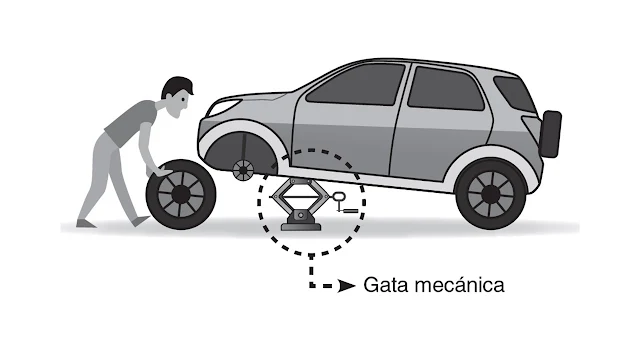
07.- La gata mecánica es un dispositivo que sirve para levantar una carga pesada con poco esfuerzo. Facundo utiliza este dispositivo para levantar su camioneta y cambiar una llanta.

A partir de esta situación, ¿cuál de las siguientes alternativas expresa la masa aproximada de la camioneta de Facundo?

a) 2 000 gramos.

b) 2 000 miligramos.

c) 2 000 toneladas.

d) 2 000 kilogramos.

08.- Como parte del proyecto “Unamos pueblos”, se propuso asfaltar una carretera. En el 2019, se asfaltaron 9,3 km. Esta cantidad representa la tercera parte de la longitud total de carretera propuesta en el proyecto.

En total, ¿cuántos kilómetros de carretera se propuso asfaltar en este proyecto?

a) 3,1 km

b) 9,6 km

c) 12,3 km

d) 27,9 km

Resuelve problemas de regularidad, equivalencia y cambio.

09.- Boris es fabricante de joyas. Él está confeccionando una pulsera con perlas colocadas en los vértices de pequeñas estructuras hexagonales de plata. La estructura básica que utiliza es la siguiente.

El diseño de Boris consiste en encadenar estas estructuras del modo que se muestra a continuación.

La pulsera completa debe tener 8 hexágonos de plata con sus respectivas perlas. ¿Cuántas perlas utilizará Boris en total para confeccionar la pulsera?

a) 28 perlas.

b) 34 perlas.

c) 36 perlas.

d) 48 perlas.

10.- En una clase de Arte, se exponen las hojas de trabajo de los estudiantes. Para ello, estas hojas se cuelgan de una pita utilizando ganchos de la siguiente manera.

Se ha elaborado la siguiente tabla para saber la cantidad de ganchos que se necesita según la cantidad de hojas.

¿Cuál de las siguientes expresiones permite calcular la cantidad total de ganchos “G” necesarios para colgar “n” hojas?

a) G = 4n

b) G = n + 2

c) G = 2n + 2

d) G = 4n + 2

11.- Camila desea comprar un televisor pagando una cuota inicial y el resto en cuotas mensuales iguales durante dos años. Ella llega a un acuerdo con el vendedor. Este acuerdo se representa con la siguiente expresión.

T = 200 + 50m

Si “T” es la cantidad total de dinero pagado por el televisor al transcurrir “m” meses, ¿cuál de las siguientes alternativas explica correctamente el acuerdo de Camila con el vendedor?

a) Camila pagará 50 soles de cuota inicial y 200 soles mensuales.

b) Camila pagará 200 soles de cuota inicial y 50 soles mensuales.

c) Camila pagará 250 soles de cuota inicial.

d) Camila pagará 250 soles mensuales.

12.- Leonel está confeccionando un collar muy largo a base de semillas. Para ello, está siguiendo esta secuencia.

Lee las siguientes afirmaciones. Luego, marca una X en la columna V si la afirmación es verdadera o en la columna F si es falsa.

Respuesta adecuada

El estudiante evidencia su comprensión sobre el patrón de repetición involucrado en esta situación. Establece adecuadamente la relación entre la posición que ocupa cada semilla y el tipo de semilla colocada en el collar. De este modo, responde correctamente a las seis afirmaciones propuestas.

13.- ¿Cuánto vale “x” en la siguiente ecuación?

3x − x + 4 = 5x – 8

a) x = − 6

b) x = 2

c) x = −2

d) x = 4

14.- Gabriela quiere postular a la Escuela de Oficiales del Ejército. Para ello, necesita cumplir el siguiente requisito de edad.

EDAD:

• Mínima: 15 años (*)

• Máxima: 21 años, 11 meses y 29 días (*)

(*) Computados al 31 de diciembre del año anterior al proceso.

Si “x” es la edad requerida expresada en años, ¿cuál de las siguientes expresiones representa el requisito de edad que debe cumplir Gabriela para postular?

a) 15 < x < 21

b) 15 ≤ x < 22

c) 15 ≤ x ≤ 21

d) 15 < x ≤ 22

15.- El costo por una hora de alquiler de una cabina de internet es S/1,50 y el costo por la impresión de una página es S/0,50.

Pablo tenía S/6,50. Como debía hacer una tarea, él alquiló una cabina de internet para buscar información y, luego, imprimió varias páginas. De ese modo, gastó todo el dinero que tenía.

Explica dos posibles formas en que Pablo pudo gastar todo su dinero. Precisa la cantidad de horas que alquiló la cabina y la cantidad de páginas que imprimió.

Respuesta adecuada

El estudiante establece de forma adecuada relaciones aditivas y/o multiplicativas entre los datos propuestos en la situación. Gracias a ello, propone dos formas correctas de realizar el gasto de todo el dinero (en alquiler de horas de la cabina de internet y en impresión de páginas). Puede utilizar representaciones numéricas, gráficas o verbales para expresar las diferentes maneras en las que utilizará los S/ 6,50. Por ejemplo:

• 0,5(10) + 1,5(1)

0,5(7) + 1,5(2)

• 0,5(7) + 1,5(2)

0,5(4) + 1,5(3) = 6,5

• Imprimió 4 hojas y alquiló 3 horas de cabina de internet.

• Imprimió 10 hojas y alquiló 1 hora de cabina de internet.

16.- La siguiente gráfica muestra el tiempo que hacen Pilar y Jaime en recorrer 100 metros planos en una competencia. Observa.

Según esta información, ¿cuál de las siguientes afirmaciones es correcta?

a) Jaime corrió más rápido porque a los 12 segundos pasó a Pilar.

b) Pilar ganó la competencia porque hizo un tiempo de 12 segundos.

c) Los dos llegaron juntos porque hicieron el mismo tiempo.

d) Jaime ganó la competencia porque hizo un tiempo de 16 segundos.

17.- La siguiente gráfica muestra la relación entre el tiempo que permanece abierto un caño y la cantidad de agua que se va almacenando en un depósito.

A partir del gráfico, ¿cuál de las siguientes afirmaciones no describe la relación correcta entre el tiempo y la cantidad de agua en el depósito?

a) Cuando el caño se abrió, el depósito tenía 800 ml de agua.

b) El caño vierte 50 ml de agua por minuto.

c) En 2 minutos, el caño vertió 900 ml de agua en el depósito.

d) A los 4 minutos de abrir el caño, el depósito tenía 1 000 ml de agua.

Resuelve problemas de forma, movimiento y localización.

18.- Este es el plano de calles de una ciudad.

Según el plano observado, ¿cuál de las siguientes afirmaciones de ninguna manera es correcta?

a) Las calles 22 y 24 son paralelas.

b) Las calles 28 y 23 son perpendiculares.

c) Las calles 24 y 26 son secantes.

d) Las calles 22 y 27 son perpendiculares.

19.- Dibuja en la cuadrícula un polígono que reúna las siguientes tres características. No es necesario que uses una regla.

• Que sea un pentágono.

• Que tenga algunos ángulos rectos.

• Que tenga un eje de simetría. (Dibújalo con una línea punteada).

Respuesta adecuada

El estudiante dibuja un polígono que cumple con las tres características solicitadas. Puede o no dibujar el eje de simetría.

Nota. Los trazos en el dibujo no necesariamente deben ser precisos. Sin embargo, tiene que evidenciarse que, a través del soporte dado por las cuadrículas, se están considerando todas las características solicitadas del polígono a dibujar.

20.- Observa el siguiente mapa. Al considerar las ciudades A, B y C como vértices y trazar segmentos con esos extremos, se forma un triángulo. Raquel está en la ciudad A y su hermano Ramón en la ciudad C. Ambos acuerdan reunirse en la ciudad B, que está a 30 km de la ciudad A y a 40 km de la ciudad C.

De las alternativas que se muestran, ¿Cuál no expresa un posible valor para la distancia que hay entre la ciudad A y la ciudad C?

a) 30 km

b) 40 km

c) 60 km

d) 72 km

21.- Observa los polígonos que conforman cada grupo.

¿Cuál de las siguientes afirmaciones señala una característica geométrica que corresponde a todos los polígonos del grupo A pero no corresponde a ninguno de los polígonos del grupo B?

a) Todos los polígonos son cuadriláteros.

b) Todos los polígonos tienen todos sus lados congruentes.

c) Todos los polígonos tienen dos pares lados opuestos paralelos entre sí.

d) Todos los polígonos tienen, por lo menos, un par de lados congruentes.

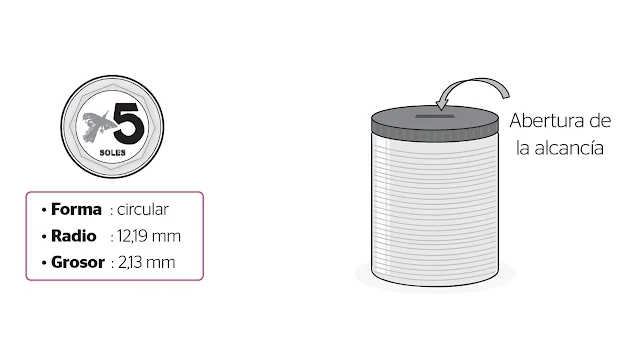
22.- Se van a fabricar alcancías para monedas de S/5. Estas serán de lata, tendrán forma cilíndrica y poseerán en la parte central superior una abertura rectangular por donde ingresarán, una por una, las monedas a guardar.

Observa a continuación las características que tienen las monedas de S/5 y la ubicación de la abertura que tendrán las alcancías.

¿Cuál de los siguientes pares de dimensiones sería el adecuado para que esta abertura permita el ingreso de las monedas?

a) Largo: 12,30 mm

Ancho: 2,1 mm

b) Largo: 12,30 mm

Ancho: 2,5 mm

c) Largo: 25 mm

Ancho: 2,5 mm

d) Largo: 25 mm

Ancho: 2,1 mm

23.- Sergio ha construido una torre con cubos. Estas son las tres vistas de la torre.

¿Cuál de las siguientes torres es la que Sergio construyó?

Respuesta C)

24.- Fredy encuentra una foto suya tomada hace 10 años. Observa.

Al verse, Fredy decide ampliar su foto para ponerla en un portarretrato. En esta ampliación, él quiere mantener la proporción entre el largo y el ancho de la foto original.

¿Cuál de las siguientes alternativas presenta las dimensiones de la foto ampliada tal como Fredy la quiere?

a) Largo: 58 mm

Ancho: 56 mm

b) Largo: 58 mm

Ancho: 58 mm

c) Largo: 60 mm

Ancho: 56 mm

d) Largo: 60 mm

Ancho: 58 mm

Resuelve problemas de gestión de datos e incertidumbre.

25.- En una escuela, se han organizado diferentes talleres deportivos. La siguiente tabla muestra parte de la información sobre los estudiantes que se han inscrito en alguno de esos talleres.

Según esta información, ¿qué porcentaje de estudiantes se ha inscrito en natación?

a) 60 %

b) 50 %

c) 30 %

d) 5 %

26.- Raúl alista su ropa de baile para ensayar danzas con sus amigos del colegio. Él puede vestirse de diferentes maneras, pero siempre debe utilizar una camisa, un pantalón y un par de zapatos. Si cuenta con 3 pantalones, 2 camisas y 2 pares de zapatos, en total, ¿de cuántas maneras diferentes podría vestirse Raúl?

a) 6 maneras.

b) 7 maneras.

c) 10 maneras.

d) 12 maneras.

27.- En una familia hay tres hermanos. Uno de ellos tiene 10 años de edad. Se sabe que el promedio de las edades de los tres es 24 años. ¿Qué edades podrían tener los otros dos hermanos? Justifica tu respuesta.

Justifica aquí tu respuesta.

Respuesta adecuada

El estudiante interpreta la noción de promedio y la relaciona con las condiciones de la situación. Usa estrategias de cálculo o estimación para determinar las posibles edades que permiten obtener el promedio dado.

Nota. Se debe priorizar la relación establecida entre las condiciones del problema y los valores asignados para las edades de los hermanos, aunque estos sean poco probables en la realidad.

Por ejemplo:

• Dado que el promedio de las edades de los 3 hermanos es 24 años y que una de las edades es 10 años, se obtiene la siguiente ecuación.

En ella, “x” e “y” (edades de los otros 2 hermanos) pueden ser 2 y 60, respectivamente. Las edades de los hermanos pueden ser 2 años y 60 años. (Esta respuesta se considera válida por las razones dadas en la nota).

• Si el promedio de las edades de 3 hermanos es 24, se asume que cada uno de ellos puede tener 24 años. Dado que uno ya tiene 10 años, las edades de los otros dos hermanos pueden ser 31 años cada uno.

• Las edades pueden ser 0 y 62 años.

• Las edades de los hermanos pueden ser 30 años y 32 años.

• Si el promedio de las edades es 24, la suma de estas debe ser 72. Hay muchos valores para las edades que cumplen con esta condición. (Estos valores se muestran en una tabla).