Matemática
Resuelve problemas de regularidad, equivalencia y cambio – Experiencia de
aprendizaje 2 Actividad 12
Proponemos afirmaciones para el uso del plástico reciclado mediante ecuaciones cuadráticas
¡Hola!
En la
actividad anterior hemos diseñado objetos con creatividad, reciclando el
plástico para promover su reducción y contribuir con el cuidado del ambiente.
En esta actividad, analizaremos la gráfica y las soluciones a las ecuaciones
cuadráticas en la fabricación de ladrillos ecoamigables para reciclar las
botellas de plástico en nuestras comunidades, con la finalidad de proponer
acciones para el cuidado del ambiente y la salud.
¡Comencemos!
Leemos y analizamos
Leemos
con atención la siguiente situación y analizamos las preguntas propuestas:
En
muchas de nuestras comunidades rurales observamos el incremento de desechos del
plástico en los ríos, campos de cultivo y pastoreo, los que contaminan el
ambiente. Frente a esta problemática, se presentan iniciativas creativas como,
por ejemplo, la de los estudiantes de la Universidad Nacional Pedro Ruiz Gallo
de Lambayeque, que presentaron prototipos de ladrillos de plástico reciclado
para la construcción de viviendas económicas y ecoamigables con el
medioambiente, para así dar un segundo uso a las botellas de plástico que
generan un problema de contaminación. Además, informaron que, para un ladrillo
de 20 cm de largo por 15 cm de ancho y 12 cm de alto, se necesita
aproximadamente unas 500 botellas plásticas, que podrían ser mezcladas con sus
tapas.
Mateo,
estudiante del 5° grado de secundaria, desea cercar un terreno de su propiedad
cuyas medidas son las siguientes: de largo mide 2 m más que el ancho y el área
mide 80 m2. Mateo se pregunta ¿cuántas botellas de plástico se reciclarán para
elaborar los ladrillos necesarios para cercar el perímetro del terreno?
Comprendemos el problema
Comentamos
el problema con nuestras propias palabras y luego respondemos las siguientes
preguntas en el cuaderno:
☺ ¿Qué se
entiende por ladrillos ecoamigables?
☺ ¿Cuáles
son las dimensiones del ladrillo fabricado por los estudiantes de la
Universidad Pedro Ruiz Gallo?
☺ ¿Cuál
es el reto que debemos responder y con qué recursos contamos para hacerlo?
Determinamos la cantidad de ladrillo para el cerco del terreno
Primer paso: Relacionamos las dimensiones
Establecemos
relaciones entre el largo, ancho y el área del terreno.
♥ Completamos
la tabla con los valores que cumplen con las condiciones del problema.
|
Largo (a) |
Ancho (b) |
Área
(m2) A = a × b |
|
6 + 2 |
6 |
8 × 6 = 48 m2 ---
No cumple. ¿Por qué? |
|
|
|
|
|
|
|
|
|
|
x |
|
♥ La
expresión algebraica para hallar el área del terreno es: _________________
Segundo paso: Expresamos el modelo matemático
Ahora
expresaremos gráficamente el modelo matemático que representa las medidas del
terreno: f (x) = x 2 + 2x
Para
graficar ingresamos al aplicativo Geometría de la tableta o celular, luego
buscamos el ícono calculador y hacemos clic.
Luego interpretamos
la gráfica de la función.
Tercer paso: Respondemos a la pregunta planteada
Empleamos
estrategias para responder a la pregunta del problema:
♥ Calculamos
la longitud de los lados del terreno con la siguiente ecuación: 80 = x2
+ 2x
---------------------
♥ Calculamos
la cantidad de ladrillos que se necesitan para cercar el terreno (escribimos
nuestros procedimientos en el cuaderno):
---------------------
♥ Calculamos
la cantidad de botellas de plástico que necesitamos reciclar para construir los
ladrillos para el cerco perimétrico (escribimos nuestros procedimientos en el
cuaderno).
---------------------
Recuerda
Resolución
de ecuaciones cuadráticas mediante la factorización:
Para
factorizar un trinomio de la forma: x2 + bx + c
Paso 1:
encuentren dos números enteros, r y s, cuyo producto será igual a c y cuya suma
será igual a b.
Paso 2:
reescriban el trinomio como x2 + rx + sx + c
Paso 3: agrupen
y apliquen la propiedad distributiva para factorizar el polinomio, los factores
resultantes serán: (x + r) y (x + s)
Entonces,
factorizando la expresión, será la siguiente:
x2
+ bx + c = (x + r) (x + s)
Si la
ecuación no se puede factorizar con facilidad, utilicen la fórmula cuadrática:
Cuarto paso: Formulamos afirmaciones sobre el reciclaje
Formulamos
3 afirmaciones sobre el reciclaje de las botellas de plástico e interpretamos
el gráfico y las soluciones de la ecuación de segundo grado.
☺
---------------------
☺ ---------------------
☺
---------------------
Afianzamos nuestros aprendizajes
Determinamos
la expresión algebraica del área de la base de una jaula en función de la
longitud de uno de sus lados
Leo la
siguiente situación:
El
Instituto Nacional de Innovación Agraria (INIA) ha capacitado a los productores
dedicados a la crianza de cuyes de las comunidades campesinas de Huancayo en
los últimos años. En estas capacitaciones, los participantes han conocido las
razas liberadas por el INIA, como la andina, la inti y la Perú. Además,
formaron parte de parte de diversas actividades sobre la producción tecnificada
y ordenada en cuanto a la alimentación, las instalaciones para la crianza, los
materiales u uso de equipos, la limpieza de espacios de producción, el
mejoramiento genético, entre otros.
Mariela
vive en el anexo Inay Saños Chaupi del distrito de El Tambo, en la provincia de
Huancayo, Junín. Está contenta porque su papá, quien participó de estas
capacitaciones, va a construir una jaula para la crianza de los cuyes que
tienen con el fin de emprender una pequeña microempresa para mejorar los
ingresos de la familia. Juan tiene 16.8 m de alambre de malla para cercar todo
el borde de la jaula y Mariela le siguiere que la base sea de forma
rectangular. ¿Cómo determino la expresión algebraica que permita obtener el
área de la base de la jaula que construirá el papá de Mariela?
Reflexionamos sobre nuestro aprendizaje
Es
momento de reflexionar sobre lo aprendido.
☺ ¿Qué
situaciones nos favorecieron para lograr el propósito de aprendizaje? ¿Cuáles
nos resultaron difíciles?
☺ ¿Qué
hicimos para superarlas? ¿Cuál es la importancia de las ecuaciones cuadráticas
en nuestra vida cotidiana?
Autoevaluación
Es
importante autoevaluarnos y reconocer nuestros avances, para lo cual nos
apoyaremos en los criterios de evaluación. Luego, nos plantearemos cómo mejorar
y le comentamos nuestras dificultades a nuestra profesora o nuestro profesor
para recibir su orientación.
|
Criterios
de evaluación |
Lo logré |
Estoy en proceso de lograrlo |
¿Qué puedo hacer para mejorar mis
aprendizajes? |
|
Establezco
relaciones entre datos y valores desconocidos de las dimensiones del terreno
y las transformo a ecuaciones cuadráticas. |
|
|
|
|
Expreso
con diversas representaciones gráficas y tabulares las dimensiones del
terreno, para interpretar la solución o soluciones de una ecuación
cuadrática. |
|
|
|
|
Combino
estrategias para solucionar ecuaciones cuadráticas y determinar la cantidad
de ladrillos y botellas de plástico que se reciclarán para cercar el terreno. |
|
|
|
|
Planteo
afirmaciones sobre el reciclaje de las botellas de plástico, con argumentos
basados en las soluciones de una ecuación cuadrática. |
|
|
|



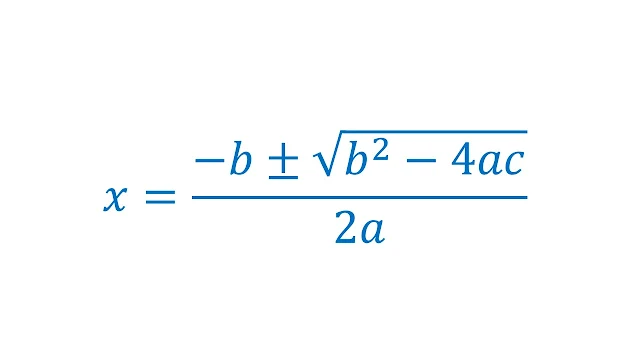

Publicar un comentario
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.