Lógica De Clases

La lógica de clases estudia la proposición lógica fundamentando la pertenencia o no pertenencia de un elemento o individuo u objeto específico  por poseer una determinada propiedad o característica.​ Sobre esta lógica se precisa como modelo científico la teoría matemática de conjuntos.

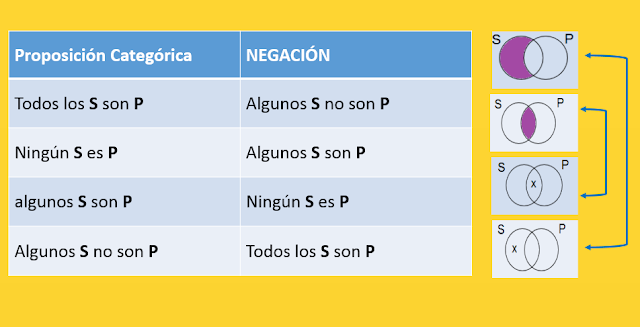
Para todos los problemas que voy a proponer, para encontrar las soluciones emplearé esta tabla en la cual se encuentra los gráficos de los diagramas de Venn para facilitar su interpretación y en forma paralela también usaré el álgebra de Boole referente a las relaciones con el conjunto vacío.

El color morado representa al conjunto vacío, cuando aparece el elemento "x"  significa que el conjunto tiene elementos específicos y si no aparece ninguno de estos características indica que falta información.

INFERENCIAS LÓGICAS

01. A partir de las siguientes premisas:

• Todos los exalumnos del colegio C son norteños, a excepción de uno que es pelirrojo.

• Ningún pelirrojo es músico.

¿Cuál de los siguientes razonamientos es correcto?

SP ̅=∅: Todos los exalumnos del colegio C son norteños

SP≠∅ : a excepción de uno que es pelirrojo

Conclusión:

SP=∅ : Ningún pelirrojo es músico.

02. Si consideramos que:

“Todos los artistas son ególatras y algunos artistas son indigentes”.

Se puede afirmar:

MP ̅=∅: Todos los artistas son ególatras 

MS≠∅ : algunos artistas son indigentes

Conclusión:

SP ̅≠∅ : Algunos indigentes son ególatras.

03. Qué se puede inferir de:

Si ningún A es B, y algunos B son C.

PM=∅: ningún A es B

MS≠∅ : algunos B son C

Conclusión:

SP ̅≠∅ : Algunos C no son A 

04. Qué se puede inferir de:

     Si todos los poetas son soñadores, y ningún soñador es racional.

SM ̅=∅: todos los poetas son soñadores

MP=∅ : ningún soñador es racional

Conclusión:

SP=∅  : Ningún poeta es racional

05. Inferir la conclusión de:

Todos los hombres son mortales.

Todos los peruanos son hombres.

MP ̅=∅: Todos los hombres son mortales

SM ̅=∅: Todos los peruanos son hombres

Conclusión:

SP ̅=∅: Todos los peruanos son mortales

NEGACIÓN DE PROPOSICIONES

veamos la tabla:

06. Dadas las proposiciones:

a.- “Todos los soldados son valientes”.

     b.- “Ningún chofer es distraído”

PROPOSICIONES EQUIVALENTES

Aquí tenemos las siguientes equivalencias:

07. Determina la equivalencia de:

Ningún hombre es inmortal.

Por lo tanto la equivalencia es:

Todos los hombres son mortales.

08. Indique la proposición equivalente a:

Todos los no deportistas son no atletas.

Por lo tanto la equivalencia es:

Todos los atletas son deportistas.

09. ¿Qué alternativa muestra una proposición equivalente a:       

“Ningún diplomático es descortés”?

S: diplomático

P: Cortez.

Estructura lógica: Ningún S es P ̅

Forma Booleana: SP ̅=∅ : Todos los S son P

 Por lo tanto la equivalencia es: Todo diplomático es cortez.

CASO ESPECIAL:

10.- Hallar las equivalencias de:

       Todos los primos no son impares

       S:primos

       P: impares.

      ~(Todos los S son P)

      ~(SP  ̅=∅)  →S"P"  ̅≠∅

 Por lo tanto la equivalencia es: Algunos "primos no son impares."

 CLIC PARA VER EL VÍDEO: