Prueba Diagnóstica 4 grado de secundaria de Matemática
Esta prueba contiene 28 preguntas: 24 de opción múltiple, 3 de respuesta abierta extensa (RAE) y 1 de respuesta abierta corta (RAC). Las respuestas de los estudiantes permitirán conocer el estado de sus aprendizajes en el momento actual.
Resuelve problemas de cantidad.
01.- En una institución educativa, se realizó una
encuesta a todos los estudiantes de 4.° grado de secundaria sobre qué carreras
desean seguir cuando terminen sus estudios. Los resultados obtenidos se
muestran en el siguiente gráfico.
A partir
del gráfico, es correcto afirmar que
a) los
estudiantes que prefieren Derecho y Administración representan ½ del total de
estudiantes.
b) los
estudiantes que prefieren Contabilidad representan 1/20 del total de
estudiantes.
c) los
estudiantes que prefieren Administración representan 1/25 del total de
estudiantes.
d) los
estudiantes que prefieren Ingeniería y Medicina representan 1/50 del total de
estudiantes.
02.- Víctor necesita comprar una computadora. Por
eso, ha decidido aprovechar la siguiente oferta de una tienda de
electrodomésticos.
Si
Víctor paga con su tarjeta de crédito SÚPER, ¿cuánto pagará por la computadora?
a) S/ 300
b) S/
420
c) S/ 1
050
d) 1 080
03.- Un agricultor cosecha papa amarilla tumbay y
la divide en tres calidades: primera, segunda y tercera. Las papas de primera
son maduras, de tamaño regular y de buen color. Las papas de segunda también
son maduras, pero tienen algunas picaduras. Por su parte, las papas de tercera
son muy pequeñas y, en su mayoría, están partidas. Por estas razones, los
precios de las papas son distintos. Observa la tabla:
Sobre la
base de esta información, señala cuál de las siguientes afirmaciones es falsa.
a) El
precio de la papa de segunda es 17 centésimos de sol mayor que el precio de la
papa de tercera.
b) El
precio de la papa de primera puede leerse como 156 centésimos de sol.
c) El
precio de la papa de tercera equivale a 95 décimos de sol.
d) El
precio de la papa de tercera se puede leer como 9 décimos y 5 centésimos de
sol.
04.- Entre los meses de marzo y abril, una
municipalidad repartió canastas de víveres a familias de muy bajos recursos.
Durante el mes de marzo, repartió 3/7 de las canastas que tenía. Luego, en la
primera quincena de abril, repartió 2/5 de lo que quedaba. Tras ello, quedaron
420 canastas en el almacén de la municipalidad. ¿Cuántas canastas tenía la
municipalidad al inicio de la repartición?
a) 2 450
b) 1 225
c) 595
d) 564
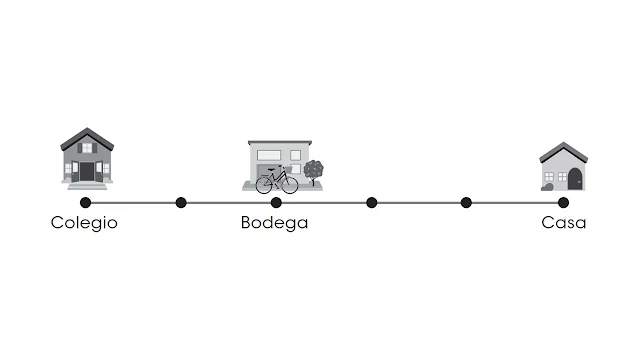
05.- En el siguiente gráfico se muestra el
recorrido en línea recta que hace Rosa del colegio a su casa. Observa.
Un día,
Rosa sale del colegio en dirección a su casa, recorre una parte del camino y se
detiene en una bodega. En esta situación, ¿cuál es la relación entre la
distancia recorrida por Rosa del colegio a la bodega y la distancia que le
falta recorrer?
a) La
distancia recorrida es 2/3 de la distancia que le falta recorrer.
b) La
distancia recorrida es 2/5 de la distancia que le falta recorrer.
c) La
distancia recorrida es 3/5 de la distancia que le falta recorrer.
d) La
distancia recorrida es 5/2 de la distancia que le falta recorrer.
06.- Observa los siguientes números.
Luego de
observar estos números, Fernando afirma lo siguiente.
“De estos cuatro números los dos últimos
no pueden convertirse en fracción porque tienen infinitas cifras decimales”
¿Estás
de acuerdo con Fernando? Sí No (Marca tu respuesta con una X)
¿Por
qué? Justifica tu respuesta.
Respuesta
adecuada
El
estudiante asume una postura (implícita o explícita) dando a entender que NO
está de acuerdo con Fernando. Explica que dichos números se pueden expresar
como fracción. En su respuesta, se evidencia la noción de equivalencia entre
números racionales representados como fracción o como expresiones decimales
(periódico puro o periódico mixto), o el estudiante podría usar algún
procedimiento (algoritmo), o brindar algún ejemplo para sustentar su respuesta.
Por ejemplo:
• No
estoy de acuerdo, porque todos los números cuya parte decimal contiene cifras
que se repiten infinitamente son números racionales, y se conocen como
decimales periódicos puros y mixtos. Todos estos tienen fracción generatriz.
(Sustenta usando su comprensión de los racionales).
• No
estoy de acuerdo, porque 0,72 con periodo en 72 se escribe como: 72/99 o bien
se escribe como alguna fracción equivalente, por ejemplo 8/11. (Sustenta su
respuesta ejemplificando solo con alguno de los decimales periódicos).
•
Fernando se equivoca porque para los dos últimos números ocurre lo mismo que con
el número 1/3, cuyo valor decimal es 0,33333...; en este número la cifra 3 se
repite infinitamente y se puede expresar como 1/3, la cual se llama fracción
generatriz.
• El
estudiante responde:
•
0,7272...= 8/11
•
0,088888...= 4/45
(Asume
una postura implícita y evidencia cierto sustento al presentar como respuesta la
fracción generatriz de los dos últimos decimales).
Resuelve problemas de regularidad,
equivalencia y cambio.
7.- Las siguientes boletas muestran parte de la
información de las compras de manzanas y duraznos que hizo Julio en dos
semanas. Durante este tiempo, el precio por kilogramo de estas frutas no varió.

De
acuerdo a la información mostrada, ¿cuál es el precio que pagó Julio por cada
kilogramo de estas frutas?
a) 1 kg
de manzanas: 8 soles.
1 kg de duraznos: 6 soles.
b) 1 kg
de manzanas: 2 soles.
1 kg de duraznos: 12 soles.
c) 1 kg de
manzanas: 4 soles
1 kg de duraznos: 9 soles.
d) 1 kg
de manzanas: 6 soles.
1 kg de durazno: 6 soles.
8.- Un agricultor alquila un tractor a sus vecinos
con el fin de obtener ingresos adicionales. Él publicó el siguiente aviso.
Si “x”
es el número de horas de uso del tractor e “y” representa el valor total a
pagar por el alquiler, ¿qué expresión representa el valor total a pagar por el
alquiler de este tractor en relación con la cantidad de horas de uso?
a) y =
20x + 60
b) y =
20x − 60
c) y =
60x + 20
d) y =
80x
9.- Mónica pliega una hoja de papel varias veces y
cuenta la cantidad total de rectángulos más pequeños que se forman con los
dobleces. Observa.
Halla la
expresión algebraica que relaciona la cantidad de plegados en la
hoja con la cantidad total de rectángulos más pequeños que se forman en
ella.
Escribe
aquí tu procedimiento y respuesta.
Respuesta
adecuada
El
estudiante hace explícita, en su respuesta, la relación (no necesariamente
algebraica) entre la cantidad de plegados y de rectángulos más pequeños
obtenidos. La expresión construida evidencia la interpretación del patrón
involucrado en la situación, ya sea como potencia de base 2 que expresa la
cantidad de rectángulos pequeños obtenidos o como factor 2 asociado a la
cantidad de plegados realizados. El estudiante expresa su respuesta con
representaciones verbales, numéricas, gráficas o algebraicas. Por ejemplo:
• r = 2d
• Se
calcula así: n° rectángulos pequeños = 2n° de plegados
•
Cantidad de rectángulos = 2 x 2 x 2 x 2 x 2 …… según la cantidad de plegados.
• Se
calcula con 2n.
• La
cantidad de rectángulos pequeños se multiplica por dos tantas veces como
plegados se hagan. Por ejemplo, en tres plegados se tiene 2 x 2 x 2 = 8
rectángulos.
•
Continúa la serie gráfica, deduce una relación y la expresa en forma verbal.
El
número de rectángulos pequeños se obtiene elevando 2 al número de plegados.
Nota. No se
admiten como respuestas adecuadas aquellas que dicen “el doble de rectángulos”
o “2d” o cualquier otra expresión que relacione solo la cantidad de rectángulos
obtenidos entre sí.
10.- Resuelve la siguiente ecuación:
(x − 2)2
= 25
Marca la
alternativa que expresa los valores que puede tomar “x” en la ecuación dada.
a) x =
7; x = 5
b) x =
−7; x = 3
c) x =
−3; x = 7
d) x =
−5; x = 5
11.- Para ir de Cusco a Machu Picchu, se puede
tomar el servicio de tren hasta Aguascalientes. El costo por este servicio se
muestra a continuación.
Un
sábado, un total de 500 personas se trasladaron mediante alguno de estos dos
tipos de servicio. Si “x” es la cantidad de personas que tomaron el servicio
económico, ¿cuál de las siguientes expresiones representa el dinero recaudado
“y” por las personas que tomaron el servicio turístico ese mismo día?
a) y =
20x
b) y =
180x
c) y =
20(500 − x)
d) y = 180(500
− x)
12.- Rubén elabora panes con harina de trigo. Para
ello compra harina en sacos de 50 kilogramos (kg). Se sabe que cada saco de
harina le rinde para elaborar 1 900 panes.
Un día
Rubén elaboró 570 panes, ¿cuántos kilogramos de harina usó para esta cantidad de
panes?
a) 38 kg
b) 15 kg
c) 3,3 kg
d) 21,6 kg
13.- Una pelota es lanzada hacia arriba. La
siguiente gráfica representa dicho movimiento.
¿Cuál de
las siguientes alternativas no expresa la información dada por la
gráfica?
a) El
valor 6 del punto (6 ; 0) representa el tiempo que demoró la pelota en subir y
caer al suelo.
b) El
punto (0 ; 0) representa el momento inicial en el que la pelota, ubicada en el
suelo, está a punto de ser lanzada al aire.
c) La
pelota demoró 5 segundos para alcanzar por primera vez una altura de 5 metros.
d) La
altura máxima alcanzada por la pelota es de 9 metros y está expresada por la
parte más alta de la gráfica.
14.- La figura sombreada que se muestra a
continuación es un cuadrado cuya medida de sus lados está expresada en
centímetros.
Según lo
mostrado, ¿cuál es el área de la región sombreada en centímetros cuadrados?
a) a2
+ 25
b) a2
+ 10a + 25
c) 4a +
20
d) 2a +
10
15.- Lucila quiere conocer el peso de unos bloques
de madera. Ella sabe que cada bloque tiene el mismo peso. Para averiguar cuál
es el peso de cada bloque de madera, ella utiliza una balanza y dos pesas de
metal: una de 500 g y otra de 1 400 g. Observa.
Según lo
mostrado, respecto al peso de cada bloque de madera, ¿cuál de las
siguientes afirmaciones es verdadera?
a) Es
menor a 500 g.
b) Está
entre 400 y 500 g.
c) Es
mayor a 1400 g.
d) Está
entre 500 y 700 g.
Resuelve problemas de forma, movimiento
y localización
16.- Observa las cinco cartulinas que tienen forma
rectangular. Algunas de estas cartulinas son semejantes a la cartulina 1,
esto quiere decir que sus lados tienen medidas proporcionales a dicha
cartulina.
De
acuerdo a lo mostrado ¿qué cartulina no es semejante a la cartulina 1?
a)
Cartulina 3.
b)
Cartulina 2.
c)
Cartulina 4.
d)
Cartulina 5.
De las
alternativas que se muestra, ¿cuál no expresa un posible valor para la
distancia que hay entre ambos bomberos?
a) 6,1 m
b) 35,5
m
c) 25 m
d) 10 m
18.- Teresa compra una pecera que tiene forma de
prisma recto y base rectangular. La siguiente imagen muestra las dimensiones de
esta pecera.
Tal como
se observa, Teresa echa agua en la pecera hasta 10 cm por debajo de su borde
superior, ¿qué volumen ocupará el agua?
a) 150
cm3
b) 1 200
cm3
c) 36
000 cm3
d) 48
000 cm3
19.- El siguiente plano representa el territorio de
Bolivia.
Cada
cuadradito tiene 30 000 km2 de área.
a) Entre
260 000 km2 y 370 000 km2.
b) Entre
900 000 km2 y 1 300 000 km2.
c) Entre
500 000 km2 y 700 000 km2.
d) Entre
1 200 000 km2 y 2 000 000 km2.
20.- Diversos productos comerciales se envasan en
cajas con forma de prismas rectos.
Observa
la forma de estos envases.
Marca
una X en cada afirmación según corresponda a las propiedades de los prismas
rectos.
Respuesta adecuada
El
estudiante logra evaluar, de forma acertada, la verdad o falsedad de las cinco
afirmaciones respecto de los prismas rectos. Por ejemplo:
21.- Sergio ha construido una torre con cubos.
Estas son las tres vistas de la torre.
¿Cuál de
las siguientes torres es la que Sergio construyó?
Respuesta:
C
22.- Todas las figuras que se muestran a
continuación representan diseños de ventanas con forma de trapecios.
Considerando
estas figuras, ¿qué alternativa describe de forma correcta las características específicas
de los trapecios?
a)
Tienen un par de lados opuestos paralelos entre sí.
b)
Tienen lados opuestos de igual longitud.
c)
Tienen todos sus lados de diferente medida.
d)
Tienen dos pares de lados opuestos paralelos entre sí.
Resuelve problemas de gestión de
datos e incertidumbre.
23.- Los estudiantes de 5.° grado de secundaria
están organizando su graduación. Para elegir al estudiante que dará el discurso
de despedida, han decidido realizar un sorteo.
Con ese
objetivo, colocan dentro de una caja un conjunto de tarjetas de igual forma y
tamaño. Estas tarjetas contienen los nombres de los estudiantes propuestos y
las secciones a las que ellos pertenecen. Observa.
¿Qué
probabilidad hay de que, al sacar una tarjeta, el estudiante elegido sea del
5.° B?
a) 1/3
b) 2/5
c) 2/3
d) 3/5
24.- En una escuela, se han organizado diferentes
talleres deportivos. La siguiente tabla muestra parte de la información sobre
los estudiantes que se han inscrito en alguno de esos talleres.
Según
esta información, ¿qué porcentaje de estudiantes se ha inscrito en natación?
a) 60%
b) 50%
c) 30%
d) 5%
25.- En el siguiente gráfico, se muestra la
variación de la cantidad total de personas contagiadas por un virus durante los
primeros quince días de abril.
¿Cuál de
las siguientes conclusiones no corresponde a la información brindada?
a) El
mayor incremento del total de personas contagiadas por día se dio entre el 12 y
el 13 de abril.
b) En
los primeros cuatro días de abril, el incremento del total de personas
contagiadas por día no superaba los 300.
c) El 8
de abril, la cantidad total de personas contagiadas casi se duplicó respecto
del 5 de abril.
d) Del 8
al 12 de abril, el incremento del total de personas contagiadas fue superior a
800 por día.
26.- Carlos y Sofía juegan a lanzar un dado en
igualdad de condiciones. Sobre la base de su frecuencia relativa, la
probabilidad de que Carlos gane es 0,25. A su vez, la probabilidad de que Sofía
gane es 0,6.
Según
esta información, ¿cuál de las siguientes afirmaciones es correcta?
a) Es
más probable que gane Sofía.
b) Es
más probable que gane Carlos.
c) Es
imposible que Carlos gane.
d) Es
seguro que Sofía ganará.
27.- El trigo es uno de los alimentos básicos para
la industria de la panificación. Es también el tercer cereal más producido en
el Perú después del maíz y del arroz. En estos últimos años, su producción ha
ido incrementándose de manera sostenida. Observa esta tabla.
¿Cuánto
aumentó (en miles de toneladas) el promedio de producción de trigo en el
periodo 2016 - 2018 respecto del periodo 2013 - 2015?
Escribe
aquí tu procedimiento y respuesta.
Respuesta
adecuada
El
estudiante muestra un procedimiento correcto en el cual utiliza diversas
estrategias para encontrar el aumento del promedio de producción en los dos
periodos dados. Su respuesta puede ser redondeada a miles de toneladas. Además,
puede evidenciar error u omisión de las unidades involucradas (no expresa su
respuesta en miles de toneladas o no indica unidades). Por ejemplo:
•
Promedio 2016 al 2018: (156 + 160 + 162)/3 = 478/3 = 159,33
Promedio
2013 al 2015: (143 + 147 + 154)/3 = 444/3 = 148
Entonces:
159,33 – 148 = 11,3
Respuesta:
el promedio aumentó en 11,3 miles de toneladas por hectárea.
•
Producción 2016 al 2018: 156 + 160 + 162 = 478
Producción
2013 al 2015: 143 + 147 + 154 = 444
Entonces:
478 – 444 = 34 34/3 =
11,3333333 = 11
Respuesta:
el promedio aumentó en 11 000 toneladas por hectárea.
• El
estudiante responde:
El
promedio es 159,3.
Respuesta:
era 148 y subió a 159,3. Entonces, hubo un aumento de 11,3 miles de toneladas.
•
Promedio 2016 al 2018 : 159,3 Promedio 2013 al 2015: 148
Entonces: 159,33 – 148 = 11,3
Respuesta:
el promedio aumentó en 11,3 toneladas por hectárea.
(Confunde
miles de toneladas con toneladas).
•
Producción 2016 al 2018 : 478 Producción 2013 al 2015: 444
Entonces:
478 – 444 = 34 Promedio: 34 ÷ 3 = 11,33
Respuesta:
el promedio aumentó en 11,33.
(Omite
en su respuesta la unidad que representa el valor hallado).
28.- Estas dos cajas contienen canicas del mismo
tamaño, pero de distinto color.
Santiago
saca una canica con los ojos vendados, ¿qué caja debe elegir para tener la mayor
probabilidad de sacar una canica blanca en el primer intento?
a) La
caja B, porque tiene igual cantidad de canicas blancas, grises y negras.
b)
Cualquier caja, porque en ambas hay 3 canicas blancas.
c) La
caja A, porque más de la mitad de canicas son blancas.
d) La
caja A, porque tiene igual cantidad de canicas negras y grises.



























إرسال تعليق
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.