Prueba de Matemática de 5.° grado de secundaria
Esta prueba contiene 28 preguntas: 23 de opción múltiple, 3 de respuesta abierta extensa (RAE) y 2 de respuesta abierta corta (RAC). Las respuestas de los estudiantes permitirán conocer el estado de sus aprendizajes en el momento actual.
Resuelve problemas de cantidad
1.- En el colegio San Clemente se realizó
una encuesta a todos los estudiantes de 5.° grado de secundaria en la que se
les preguntó cómo se trasladan para asistir al colegio. El 45 % de ellos indicó
que iba caminando. ¿Qué expresión corresponde a este grupo de estudiantes que
va caminando al colegio?
a)
4/5 del total.
b)
9/20 del total.
c)
1/45 del total.
d)
45/55 del total.
2.- Carmen tiene una bandeja con panes. Algunos son cachitos y otros son integrales. Observa.
De acuerdo a los panes mostrados
en esta bandeja, ¿cuál es la relación entre la cantidad de cachitos y la
cantidad de integrales?
a) La cantidad de cachitos es 2/3
de la cantidad de integrales.
b) La cantidad de cachitos es 2/5
de la cantidad de integrales.
c) La cantidad de cachitos es 3/5
de la cantidad de integrales.
d) La cantidad de cachitos es 3/2
de la cantidad de integrales.
3.- Observa las siguientes tarjetas de números:
Ahora marca con una X las tarjetas que presenten un
número que no puede ser escrito como una fracción.
Solución
Respuesta adecuada
El estudiante logró identificar y
marcar los tres números irracionales presentes en el conjunto de números
mostrado. Puede equivocarse solo una vez al marcar como irracional un número racional.
Por ejemplo, responde:
4.- Juana está colocando mayólicas en el piso de su baño. De pronto, se da
cuenta de que le van a faltar 12 mayólicas.
En la tienda, le indican que solo
se venden mayólicas en cajas de 5 unidades. Su precio es el que se muestra en
el siguiente cartel.
¿Cuánto dinero necesita Juana
para comprar las 12 mayólicas que le faltan?
a) S/342,00
b) S/85,50
c) S/68,40
d) S/57,00
5.- En una carrera de 100 metros planos para varones, cuatro atletas han
obtenido los siguientes tiempos al finalizar la competencia.
Sobre la base de esta
información, ¿cuál de las siguientes afirmaciones es correcta?
a) Marcos ganó a Ernesto por 7
centésimos de segundo.
b) Silvio llegó 33 décimos de
segundo antes que Alexander.
c) Alexander hizo un tiempo de 1
035 décimos de segundo.
d) Ernesto hizo un tiempo de 9
segundos con 97 décimos de segundo.
6.- Beto desea comprar una cocina. En una tienda de artefactos, venden la
cocina que él quiere a S/800. Por ser la semana del ahorro, le ofrecen un
descuento del 20 %. Además, le ofrecen un descuento adicional del 10 % si paga
al contado.
Si Beto compra la cocina, toma la
oferta y además paga al contado, ¿cuánto pagará por la cocina?
a) S/240
b) S/560
c) S/576
d) S/720
7.- El transporte masivo de personas se ha vuelto una necesidad en todo el
mundo. En diversos países, se han producido e implementado trenes que alcanzan
velocidades muy altas. A continuación, se muestran las velocidades máximas
aproximadas que pueden alcanzar cuatro de los trenes más rápidos del mundo.
• El tren AGV Italo (Italia)
tiene una velocidad máxima de 360 km/h.
• El tren Maglev (China) tiene
una velocidad máxima de 7,15 km/min.
• El tren Talgo 350 (España)
tiene una velocidad máxima de 97 m/s.
• El tren Harmony (China) tiene
una velocidad máxima de 0,10 km/s.
Según esta información, ¿cuál de
los trenes es el más veloz?
a) AGV Italo.
b) Maglev.
c) Talgo 350.
d) Harmony.
Resuelve problemas de regularidad, equivalencia y cambio
8.- Max va a alquilar una grúa cuyo alquiler cuesta S/50 por hora, más S/30
de pago único para el chofer. Max sabe que solo dispone de S/480 para ese
servicio.
¿Cuántas horas podrá Max alquilar
la grúa sin que le falte dinero?
a) De 10 a más horas.
b) Hasta 10 horas.
c) De 9 a más horas.
d) Hasta 9 horas.
9.- En la posta médica de un pueblo, se presentó por primera vez una
persona con los síntomas de una enfermedad adquirida por contagio de un virus
desconocido. En los siguientes días, la cantidad de personas contagiadas
aumentó. Observa.
Si el número de contagiados sigue
el mismo patrón de los primeros cuatro días, y si no se toman las medidas
adecuadas para contrarrestar la propagación del virus, ¿cuántas personas
contagiadas en total habrá al sexto día?
a) 4 096 personas.
b) 1 024 personas.
c) 256 personas.
d) 85 personas.
10.- Fátima construye figuras con palitos de fósforo siguiendo este patrón.
¿Cuál de las siguientes
expresiones le permite a Fátima obtener “T”, que es la cantidad de palitos
necesaria para armar la Figura “n”?
a) T = 12n + 4
b) T = 4n + 12
c) T = 4n + 1
d) T = 4n
11.- En un grifo se vende dos tipos de gasolina.
Al final de un día de trabajo, el
grifo vendió 102 galones de gasolina y recaudó en total S/1 360. Siendo “x” e
“y” la cantidad de galones de gasolina de 90 y 95 octanos que se vendieron,
respectivamente, en el grifo ese día, ¿cuál es el sistema de ecuaciones que
representa esta situación?
a) 16x + 12y = 1360
x + y = 102
b) 90x + 95y = 1360
xy = 102
c) 12x + 16y = 1360
x + y = 102
d) 12x + 16y = 1360
xy = 102
12.- Sergio se dedica a la repostería. Para preparar 2 tortas de vainilla,
él empleó 10 huevos y 500 gramos de harina en total. En ambas tortas, mantuvo
la misma proporción en la cantidad de estos ingredientes.
A Sergio le acaban de hacer un
pedido de 7 tortas de vainilla iguales a las anteriores.
¿Cuántos huevos y cuántos gramos
de harina necesitará él para cumplir con este pedido?
a) 5 huevos y 250 gramos de
harina.
b) 7 huevos y 700 gramos de
harina.
c) 40 huevos y 1 000 gramos de
harina.
d) 35 huevos y 1 750 gramos de
harina.
13.- Se abre un caño que empieza a llenar un recipiente cilíndrico con un
flujo constante de agua. Después de algunos segundos, este flujo cambia. La
siguiente gráfica muestra la relación entre el nivel de agua que alcanza este
recipiente (en centímetros) y el tiempo transcurrido (en segundos). Observa.
Según esta gráfica, ¿cuál de las
siguientes alternativas describe la relación correcta entre el tiempo transcurrido y el nivel de agua en el recipiente?
a) En los 3 primeros segundos el
flujo de agua fue más intenso que en los siguientes segundos.
b) El agua alcanza el máximo
nivel del recipiente al cabo de 30 segundos.
c) En los últimos 12 segundos, el
flujo de agua ingresa con mayor intensidad hasta alcanzar los 30 centímetros de
nivel de agua.
d) Por cada segundo el nivel de
agua sube 2 centímetros.
14.- Freddy pliega una hoja de papel varias veces y cuenta la cantidad total
de rectángulos más pequeños que se forman con los dobleces. Observa.
Halla la expresión algebraica que
relaciona la cantidad de plegados en la hoja con la cantidad
total de rectángulos más pequeños que
se forman en ella.
Escribe aquí tu procedimiento y
respuesta.
Solución
Respuesta adecuada
El estudiante hace explícita la
relación entre las variables involucradas: cantidad de plegados y rectángulos
más pequeños obtenidos. En su respuesta, que puede ir acompañada de un
procedimiento, se evidencia el patrón que involucra la potencia de base 2 y que
se representa mediante expresiones algébricas (las cuales evidencian la relación
entre la cantidad de plegados y la de rectángulos pequeños formados). Por ejemplo:
Muestra la relación correcta sin
procedimiento.
• y = 2 x
• La expresión es 2 x,
ya que la cantidad de rectángulos más pequeños es una potencia de 2, donde “x”
es la cantidad de plegados.
• Siendo “a” la cantidad de
plegados y “b” la cantidad de rectángulos más pequeños, se obtiene la siguiente
expresión: b = 2 a.
Muestra la relación correcta con
procedimiento.
La cantidad de rectángulos es 2n
luego de hacer “n - 1” plegados a partir del primer plegado.
15.- La siguiente gráfica muestra la relación entre el tiempo (en minutos)
que permanece abierto un caño y la cantidad (en mililitros) de agua que se va
almacenando en un depósito.
A partir de la gráfica, ¿cuál de
las siguientes alternativas no describe la relación correcta entre el tiempo y la cantidad de agua en
el depósito?
a) Cuando el caño se abrió, el
depósito tenía 800 ml de agua.
b) El caño vierte 50 ml de agua
por minuto.
c) En 2 minutos, el caño vertió
900 ml de agua en el depósito.
d) A los 4 minutos de abrir el
caño, el depósito tenía 1 000 ml de agua.
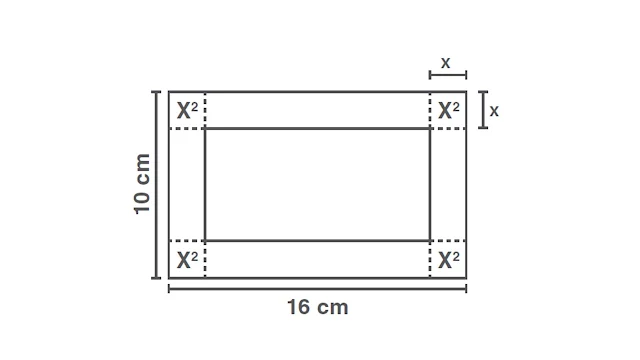
16.- Ramiro quiere construir una caja sin tapa a partir de un pedazo de
cartón rectangular con las dimensiones que se ven en la figura A. Para
lograrlo, recorta cuadrados idénticos en cada esquina del pedazo de cartón.
Cada uno de esos cuadrados tiene “x” cm de lado. Asimismo, Ramiro dobla los
rectángulos que se forman en el cartón, tal como se muestra en la figura B.
Observa.
La caja construida por Ramiro
tiene una superficie externa total de 144 cm2. ¿Cuánto mide la altura de esta
caja?
Escribe aquí tu procedimiento y
respuesta.
Solución
Respuesta adecuada
El estudiante logra comprender la
situación y plantea relaciones numéricas o algebraicas que le permiten
encontrar la altura de la caja (2 cm). También se considera adecuado si, además,
encuentra todas las dimensiones de la caja: 12 cm, 6 cm y 2 cm. Por ejemplo:
• Antes de armar la caja,
quitamos el área de los cuadrados de las esquinas; debe resultar 144 cm2
(la superficie total):
160 - 4x2 = 144→ x = ±2
Por tanto, dado que x > 0, la
altura de la caja, mide 2 cm.
• Al sumar la superficie de cada
una de las partes de la caja, debe resultar 144 cm2. Se tiene 2(x)(10 - 2x) +
2(x)(16 - 2x) + (10 - 2x)(16 - 2x)= 144
Resolviendo esa ecuación, se
obtiene que x = 2. Es decir, la altura mide 2 cm.
• Las dimensiones de la caja son
12 cm, 6 cm y 2 cm porque se verifica que la superficie total de la caja es 144
cm2.
Si x = 2, entonces:
2(12cm2) + 2(24cm2)
+ 72cm2 = 144 cm2
• 160 - 4x2 = 144→ x =
±2. Por lo tanto: x = 2
Resuelve problemas de forma, movimiento y localización
17.- Rubén está diseñando una escalera cuya inclinación será de 37° respecto
del suelo. Para ello, coloca dos parantes perpendiculares al suelo: uno a la
mitad y otro al final de la escalera. Observa.
¿Cuál es la longitud del parante
más corto?
a) 90 cm
b) 120 cm
c) 160 cm
d) 180 cm
18.- Por medidas de precaución, dos bomberos se ubican a diferentes
distancias de una casa que se está incendiando: uno se ubica a 15 m de la casa
y el otro, a 20 m. De ese modo, se forma un triángulo entre ellos y la casa. Observa.
¿Qué intervalo está incluido en
el conjunto de todos los posibles valores de la distancia que hay entre los
bomberos?
a) Entre 3 m y 30 m.
b) Entre 10 m y 40 m.
c) Entre 10 m y 30 m.
d) Entre 3 m y 40 m.
19.- Observa las cinco cartulinas que tienen forma rectangular. Algunas de
estas cartulinas son semejantes a la cartulina 1, esto quiere decir que sus lados tienen medidas proporcionales a dicha
cartulina.
De acuerdo a lo mostrado ¿qué
cartulina no es semejante a la cartulina 1?
a) Cartulina 2.
b) Cartulina 3.
c) Cartulina 4.
d) Cartulina 5.
20.- Estela diseña cometas con forma de cuadriláteros. Observa sus
características.
Según lo mostrado, marca una X en
cada afirmación según corresponda a la característica que cumplen ambas formas.
Solución
Respuesta adecuada
El estudiante responde
correctamente las cinco afirmaciones respecto de las formas dadas. Respuesta
correcta:
21.- Sergio ha construido una torre con cubos. Estas son las tres vistas de
la torre.
¿Cuál de las siguientes torres es
la que Sergio construyó?
Respuesta: C
22.- Teresa acaba de comprar una pecera que tiene forma de prisma recto y
base rectangular. Ella echa agua en la pecera de tal forma que el nivel de agua
se ubica a “x” cm de su borde superior. Observa.
Si se sabe que el agua ocupa 36
000 cm3 de la pecera, ¿a cuántos centímetros del borde superior se
encuentra el nivel de agua?
a) 10 cm
b) 20 cm
c) 30 cm
d) 40 cm
Resuelve problemas de gestión de datos e incertidumbre
23.- A continuación, se muestran las estaturas en centímetros (cm) de
algunos postulantes al equipo de básquetbol de un centro educativo.
¿Cuál es el promedio de estas
estaturas?
a) 165 cm
b) 160 cm
c) 157,5 cm
d) 154,6 cm
24.- Una olimpiada escolar de matemática consta de cuatro fases. En cada
fase, un concursante puede obtener 120 puntos como máximo.
Los organizadores de la olimpiada
han decidido premiar a los participantes que obtengan un promedio de 85 puntos
como mínimo en las cuatro fases.
Nancy ha obtenido los siguientes
puntajes en las tres primeras fases.
¿Qué puntaje debe obtener Nancy
como mínimo en la cuarta fase de la olimpiada para recibir el premio?
a) 79 puntos.
b) 85 puntos.
c) 102 puntos.
d) 120 puntos.
25.- En la siguiente tabla incompleta, se muestran los resultados de una
encuesta correctamente realizada sobre las preferencias de votación para elegir
a una junta directiva vecinal.
¿Cuál es la probabilidad de que
salga elegida la lista Avancemos?
a) 0,16
b) 0,20
c) 0,44
d) 0,80
26.- En el siguiente gráfico, se muestra la variación de la cantidad total de
personas contagiadas por un virus durante los primeros quince días de abril.
¿Cuál de las siguientes
conclusiones no corresponde a la información brindada?
a) El mayor incremento del total
de personas contagiadas por día se dio entre el 12 y el 13 de abril.
b) En los primeros cuatro días de
abril, el incremento del total de personas contagiadas por día no superaba los
300.
c) El 8 de abril, la cantidad
total de personas contagiadas casi se duplicó respecto del 5 de abril.
d) Del 8 al 12 de abril, el
incremento del total de personas contagiadas fue superior a 800 por día.
27.- Milagros y Felipe juegan a lanzar una moneda y un dado,
respectivamente. Milagros dice que, si ella lanza una moneda y cae cara, ella
gana. Felipe dice que, si él lanza un dado ordinario y le sale 3 o menos de 3,
él gana. ¿Quién de los dos tiene mayor probabilidad de ganar? ¿Por qué?
Explica aquí tu razonamiento y
escribe tu respuesta.
Solución
Respuesta adecuada
El estudiante menciona (implícita
o explícitamente) que Milagros y Felipe tienen igual probabilidad de ganar, y
justifica su respuesta. En su justificación, se observan expresiones
(numéricas, simbólicas o gráficas) relacionadas a determinar la probabilidad de
sucesos aleatorios. Por ejemplo:
• Ya que en la moneda hay una
cara y un sello, la probabilidad de que salga cara es del 50 %, mientras que,
en el dado, puede salir 1, 2 o 3, que son 3 de 6 números posibles. Con el dado,
la probabilidad también es 50 %. Son iguales.
• Moneda: 1/2. Dado: 3/6. Como ½ =
3/6, ellos tienen igual opción de ganar.
• Mónica y Felipe tienen la misma
probabilidad de ganar. (A continuación, se observa la justificación de la
respuesta mediante una estrategia gráfica).
28.- Al lanzar una moneda al aire, esta puede caer al suelo mostrando “cara”
o “sello”, en su parte visible.
Aurora lanzó al aire estas tres
monedas a la vez.
¿De cuántas maneras diferentes
pudieron quedar la parte visible de estas tres monedas al caer juntas, al
suelo?”
a) 9 maneras.
b) 8 maneras.
c) 3 maneras.
d) 2 maneras.





























إرسال تعليق
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.