Examen de ascenso 2021 Área Matemática Parte 2 Preguntas con Respuestas
11.- Un docente tiene como propósito que los estudiantes resuelvan problemas que involucran propiedades de los números naturales. En ese marco, les presenta el siguiente problema:
Dos hermanos, Rosa y Julio, recibieron de sus padres una pista de carrera para autos de juguete. Esta pista es cerrada y los carriles tienen la misma longitud. Al medir los tiempos, se obtuvo que el auto de Rosa demora 36 segundos en dar una vuelta y que el de Julio demora 42 segundos. Si los dos autos partieron en el mismo instante y en cada vuelta emplean los respectivos tiempos indicados, ¿cuánto tiempo transcurrirá para que coincidan nuevamente en el punto de partida?
Tres estudiantes indicaron cómo resolver el problema. ¿Quién lo hizo de forma correcta?
a) Angélica dijo: “Como los autos demoran 36 segundos y 42 segundos, entonces el tiempo en que coincidan será aquel que contiene, a la vez, un número exacto de veces a dichos tiempos”.
b) Beatriz dijo: “Para calcular el tiempo, colocamos a 36 y 42 encabezando dos columnas; luego, trazamos una línea vertical a la derecha y extraemos los factores comunes. Al multiplicarlos, tendremos el resultado”.
c) César dijo: “No creo que vuelvan a coincidir en algún momento, ya que al dar una vuelta la diferencia de sus tiempos es 6 segundos; en dos vueltas, es 12 segundos y, así, siempre irán distanciándose en cada vuelta que den”.
12.- El propósito de una sesión de aprendizaje es que los estudiantes resuelvan problemas que involucran el cálculo del interés compuesto. Una vez que ellos conformaron equipos, la docente les propuso la siguiente tarea:
Dionicio realizó un depósito de S/ 10 000 en una caja municipal a una tasa de interés del 1 % mensual capitalizable trimestralmente. Si acordó mantenerlo por el plazo de un año, ¿qué monto recibirá al finalizar dicho tiempo?
Al determinar que se trataba de calcular el interés compuesto, un equipo decidió utilizar la siguiente fórmula:
M = C (1 + r)t
En esta expresión, identificaron que M corresponde al monto, C toma el valor S/ 10 000 y corresponde al capital inicial, en tanto que r vale 0,03 y corresponde a la tasa de interés. Sin embargo, en cuanto al tiempo t, tres integrantes del equipo le asignaron valores diferentes. ¿Quién propone una adecuada interpretación del tiempo?
a) Alexandra dice: “Como la tasa de interés pactada se mantendrá fija por 1 año, a la variable t se le debe reemplazar por 1”.
b) Joel dice: “Como la tasa de interés está dada en forma mensual y se mantendrá durante un año, a la variable t se le debe reemplazar por 12, ya que en un año hay 12 meses”.
c) Cristina dice: “Como la tasa de interés es capitalizable trimestralmente y estará vigente durante 1 año, a la variable t se le debe reemplazar por 4, ya que en 1 año hay 4 trimestres”.
13.- Un docente tiene como propósito que los estudiantes de primer grado resuelvan problemas que involucran patrones. En ese contexto, les presenta el siguiente problema:
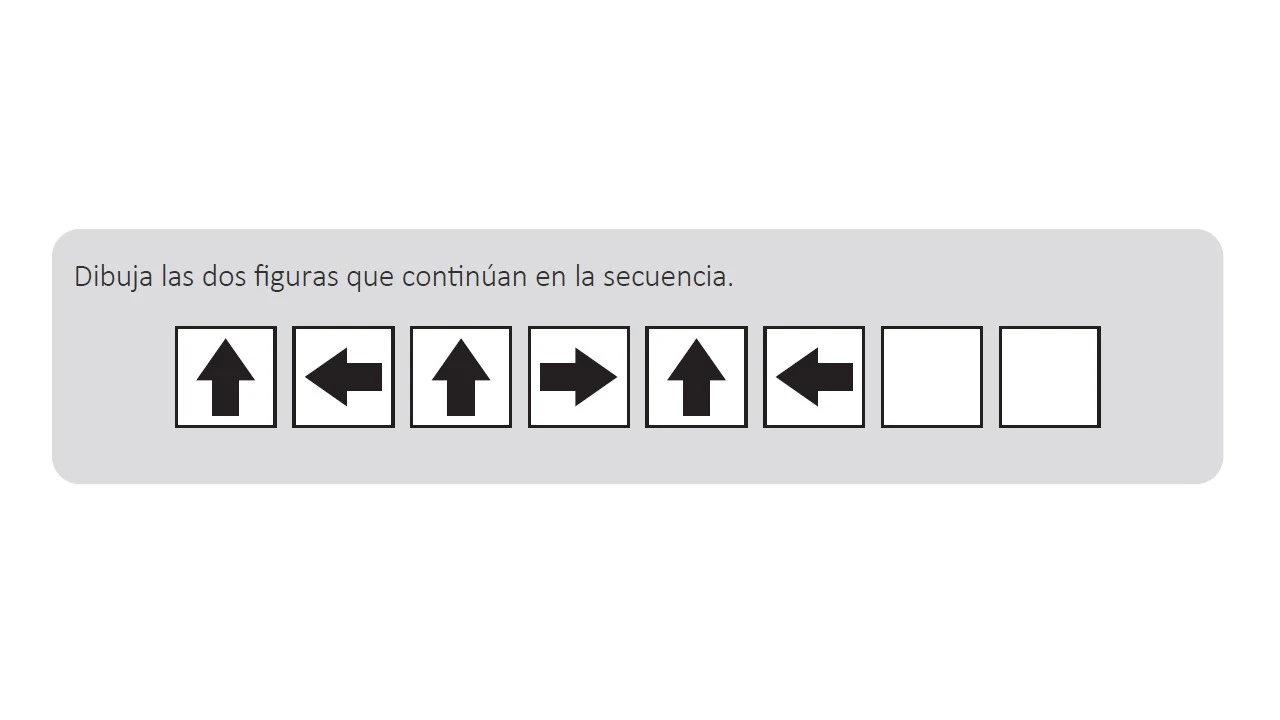
Uno de los estudiantes menciona que el séptimo término debe ser una flecha hacia arriba. Sin embargo, no puede determinar la dirección que tomaría el octavo término.
De acuerdo con lo que ha mencionado el estudiante, ¿qué logro de aprendizaje evidencia?
a) Reconoce una regla de formación que depende de la posición par o impar de los términos.
b) Reconoce que todos los términos de la secuencia lo constituyen flechas en diferentes posiciones.
c) Reconoce como regla de formación al movimiento de rotación respecto del término inmediato anterior.
14.- Dos docentes de Matemática, Vicente y Mariana, elaboran propuestas de actividades para promover la comprensión de las funciones cuadráticas por los estudiantes de tercer grado.
Como parte de una actividad, Mariana le muestra la representación de las trayectorias de dos proyectiles.
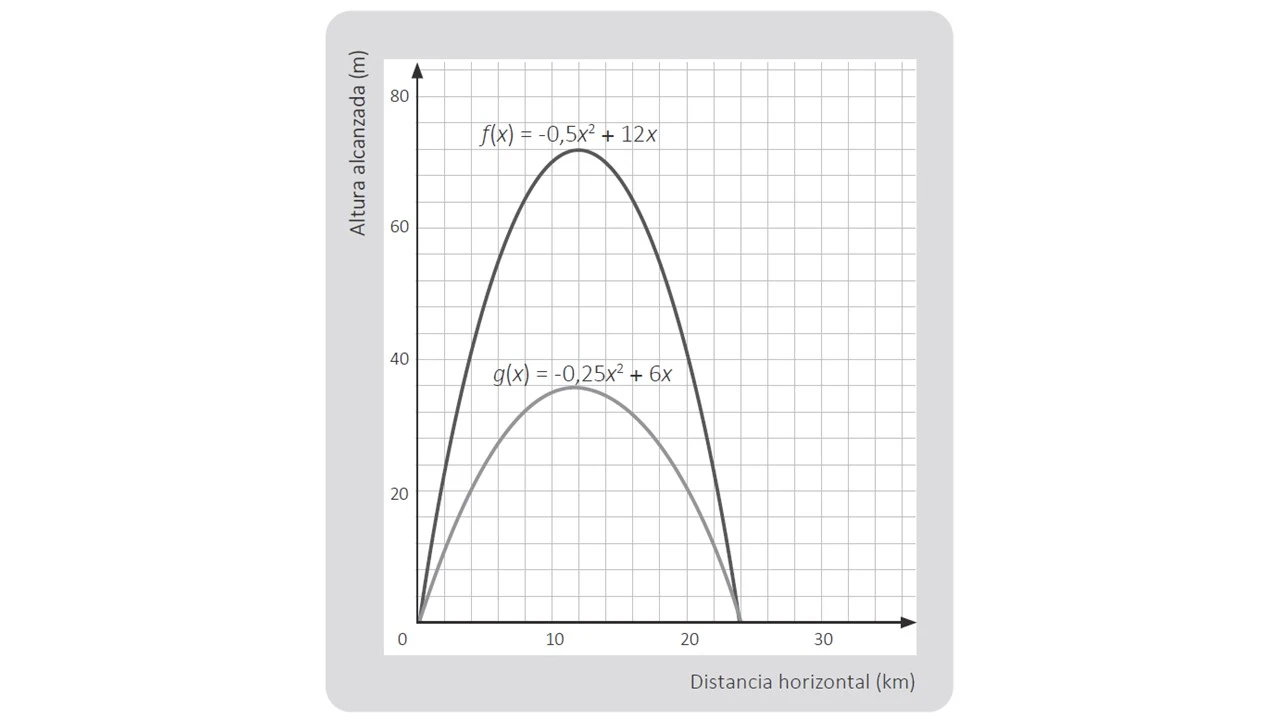
A partir de esta representación, Vicente propone tres tareas. ¿Cuál de ellas es de mayor demanda cognitiva?
a) ¿Cuál es la relación de las alturas de ambos proyectiles cuando han recorrido la misma distancia horizontal?
b) ¿Qué tipo de función representan las gráficas de la trayectoria desarrollada por los proyectiles?
c) ¿Cuánto es el valor máximo de la altura alcanzada por cada uno de los proyectiles?
15.- Durante una sesión de aprendizaje, con el propósito de que los estudiantes interpreten y representen funciones afines, un docente les propuso la siguiente tarea:
Graficar la función f cuya regla de correspondencia es f(x) = 2x + 1, donde x es un número real.
Como respuesta, un estudiante elaboró la siguiente gráfica:
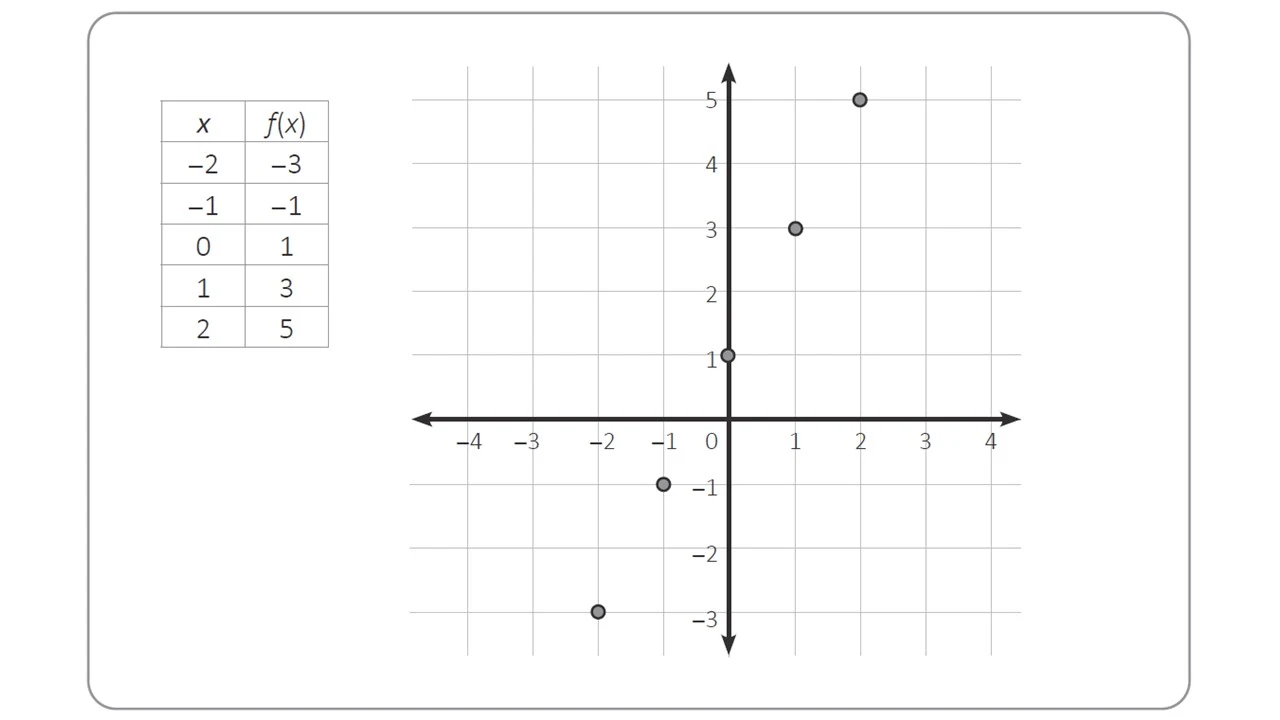
¿Cuál de las siguientes acciones pedagógicas es más pertinente para brindar retroalimentación al estudiante de modo que reflexione sobre su representación?
a) Preguntarle si esos puntos corresponden a una recta. Luego, mencionarle que tal recta presenta una pendiente y un punto de corte con el eje vertical. Finalmente, decirle que se trata de la gráfica de una función afín.
b) Preguntarle qué significa que x sea un número real. Luego, indicarle que es correcto que haya tomado esos valores para x, pero que debió haber tomado otros más. Finalmente, pedirle que una los puntos y trace una línea continua.
c) Preguntarle si, en los reales, solo se admiten valores enteros o si hay otros más. Luego, en caso de que considere esos otros valores, preguntar si la gráfica sería con saltos o sería continua. Finalmente, preguntar por la forma de la gráfica.
16.- Con respecto al uso del lenguaje algebraico en la formulación simbólica de la regla de formación de sucesiones numéricas, ¿cuál de las siguientes afirmaciones es correcta?
a) Facilita examinar regularidades en una sucesión numérica.
b) Garantiza el descubrimiento de la regla de formación.
c) Evidencia un mayor nivel de generalización.
17.- Durante una sesión de aprendizaje, un docente presenta la gráfica de un sistema de inecuaciones lineales para valores no negativos.
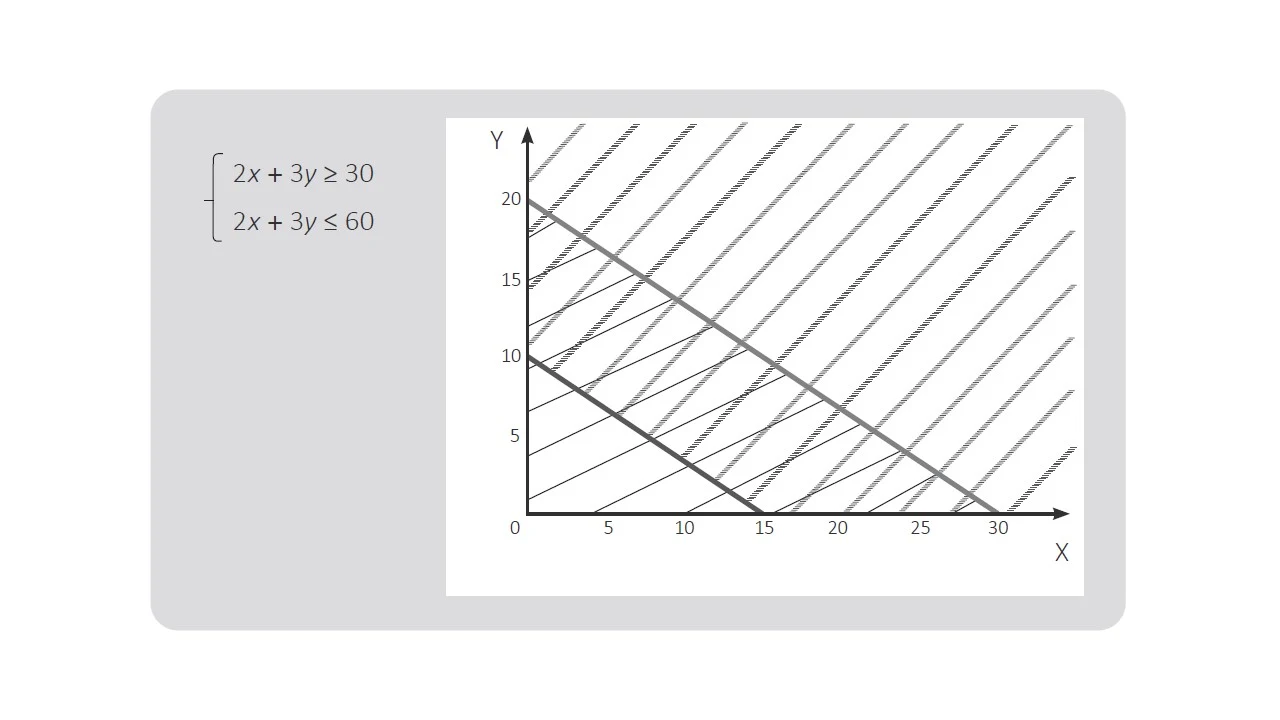
El docente busca promover que los estudiantes interpreten la gráfica del sistema de inecuaciones. ¿Cuál de los siguientes grupos de preguntas es más pertinente para lograr dicho propósito?
a) ¿Qué representan las regiones generadas por cada inecuación? ¿Qué representan los puntos de la intersección de las regiones?
b) ¿Qué tipo de cuadrilátero es la región que representa la intersección de las regiones? ¿Qué puntos del gráfico corresponden a sus vértices?
c) ¿Cuáles son los puntos de intersección entre los ejes y las rectas que limitan las regiones? ¿Qué puntos pertenecen a la intersección de las regiones?
18.- Una docente tiene como propósito evaluar que los estudiantes modelen algebraicamente situaciones de la vida cotidiana. Para ello, propuso el siguiente problema:
Un tanque tiene una capacidad de 4000 litros de agua y se abastece mediante un caño por el cual fluyen 25 litros de agua por minuto.
Si “V” es la cantidad de agua que hay en el tanque y “t” es el tiempo en minutos, representa algebraicamente una relación que permita calcular la cantidad de agua que contiene el tanque luego de haber transcurrido “t” minutos desde el instante en que se abre el caño que lo abastece. Además, precisa los valores que puede tomar el tiempo “t”. Considera que, al inicio, el tanque ya disponía de 100 litros.
La docente ha elaborado la siguiente rúbrica con las descripciones de sus niveles de logro.
|
En inicio |
En proceso |
Logrado |
| Expresa una relación de igualdad entre las variables que no cumple con las condiciones del problema. | Representa algebraicamente la relación funcional entre las variables. | Representa algebraicamente la relación funcional entre las variables, precisando los posibles valores de la variable independiente. |
Al revisar lo efectuado por los estudiantes, la docente encuentra que uno de ellos realizó la siguiente representación:
V = 25t + 100t, para cualquier valor de t
De acuerdo con la rúbrica presentada, ¿qué nivel de logro corresponde a la representación realizada por el estudiante?
a) En inicio.
b) En proceso.
c) Logrado.
19.- Durante el desarrollo de una actividad, un docente entregó a los estudiantes 9 piezas de un rompecabezas y les pidió que armaran un cuadrado. Una vez realizado, él asignó las medidas de los lados de las piezas como se aprecia en la siguiente figura:
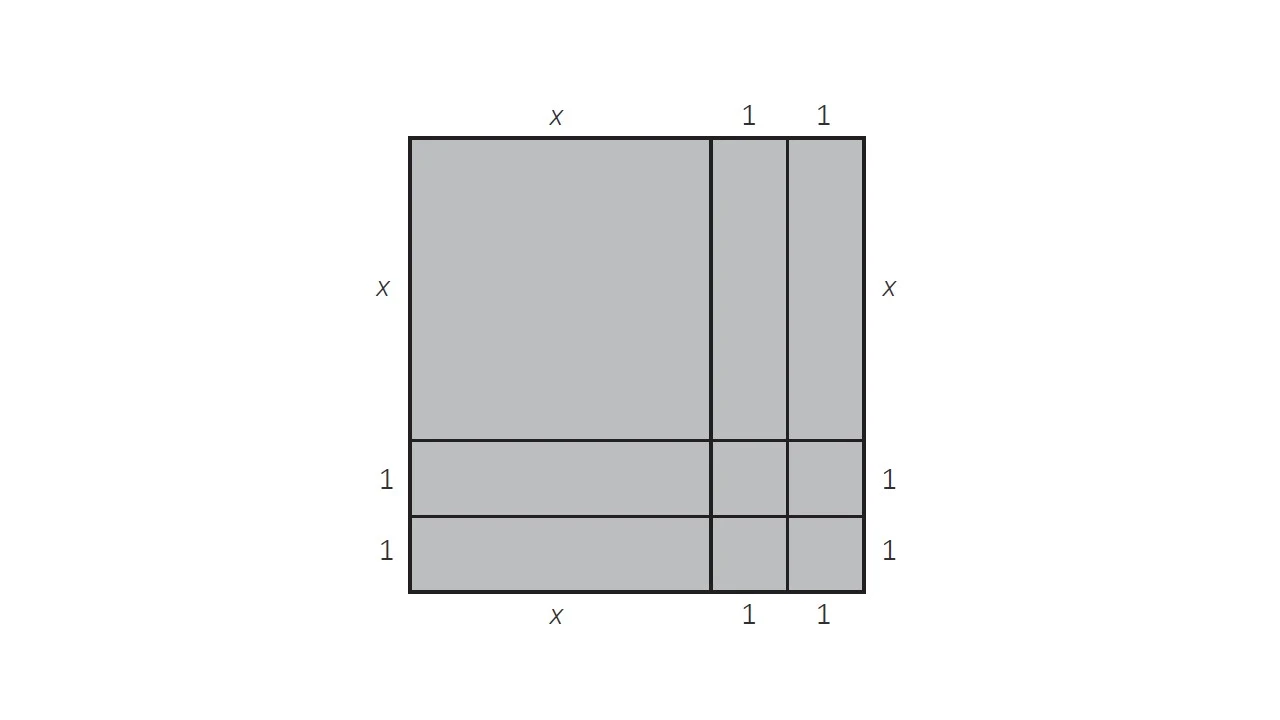
Luego, el docente les solicitó a los estudiantes lo siguiente:
• Calculen las áreas de cada una de las piezas y súmenlas para determinar la expresión que representa el área total de la figura formada.
• Determinen la medida del lado del cuadrado formado y con este valor expresen el área de dicho cuadrado.
• Respondan: ¿Qué se puede afirmar de ambas expresiones?
¿Cuál es el propósito principal de la actividad?
a) Que los estudiantes resuelvan operaciones multiplicativas con expresiones algebraicas.
b) Que los estudiantes establezcan relaciones entre las distintas expresiones algebraicas del área de una figura geométrica.
c) Que los estudiantes desarrollen su habilidad de visualización geométrica estableciendo relaciones entre las partes y el todo.
20.- Un docente propone a los estudiantes que, haciendo uso de un software matemático que sirva para graficar funciones, realicen una actividad referida a la función de la forma f(x) = ax. La secuencia de acciones propuesta es:
1. Explorar cómo es la gráfica de la función dada, si el valor de “a” es igual a 1.
2. Explorar cómo es la gráfica de la función dada, cuando el valor de “a” es mayor que 1.
3. Explorar cómo es la gráfica de la función dada, cuando el valor de “a” es menor que 1, pero mayor que 0.
4. Explicar en qué intervalos se encuentran los valores que puede tomar “a” para que dicha función sea creciente o decreciente.
Entre las siguientes alternativas, ¿cuál es el propósito principal del docente al plantear esta actividad?
a) Que los estudiantes planteen afirmaciones sobre las características de la gráfica de dicha función cuando es creciente o decreciente.
b) Que los estudiantes planteen afirmaciones sobre las condiciones que debe cumplir la base de dicha función para que sea creciente o decreciente.
c) Que los estudiantes planteen afirmaciones sobre los valores que puede tomar la variable independiente cuando dicha función es creciente o decreciente.
إرسال تعليق
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.