La función cuadrática
También
se conoce como función de segundo grado.
- El
dominio de una función cuadrática: Dom(f) = R.
- Su
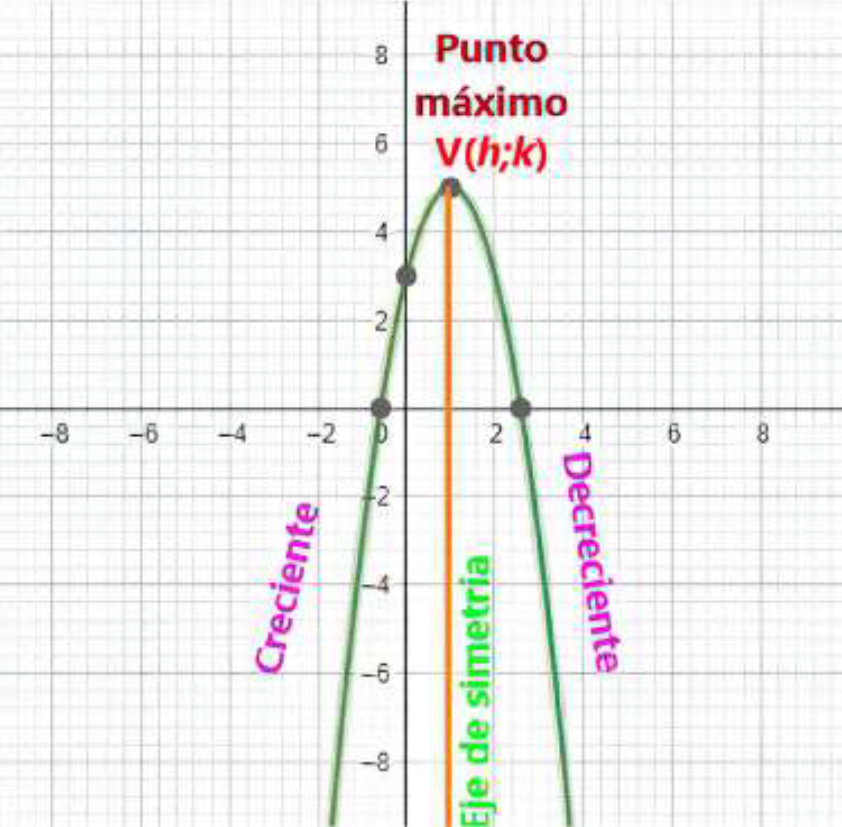
representación gráfica es una parábola.
-
Si a > 0, la parábola se abre hacia arriba y si a< 0, la parábola se abre
hacia abajo.
-
La parábola tiene un eje de simetría paralelo al eje y.
-
Tiene un vértice V(h;k), punto donde la función alcanza un máximo (si la
concavidad es hacia abajo) o un mínimo (si la concavidad es hacia arriba).
-
Si a > 0, entonces el rango es Ran(f) = [f(-b/2a); +¥[
-
Si a < 0, entonces el rango es Ran(f) = ]-¥ ; f(-b/2a)]
-
Las coordenadas del vértice son: V(h;k) = (-b/2a ; f(-b/2a)]
En
la función f(x) = ax2
- El
signo de "a" indica la concavidad de la parábola; si es positivo, la concavidad
es hacia arriba, y si es negativo, la concavidad es hacia abajo.
- El
valor absoluto de "a" modifica la abertura de las parábolas; cuanto menor es |a|,
la parábola es más abierta, y cuando mayor es |a|, la parábola es más cerrada.
Actividad de aprendizaje
Leemos la situación
Lee con atención la siguiente situación y analiza las preguntas que se plantean.
Las
estudiantes y los estudiantes de tercer y cuarto grado de educación secundaria,
están diseñando una cocina solar para reducir el uso de los combustibles contaminantes
en la preparación de sus alimentos. Esta cocina solar tiene una estructura de
madera en forma de un prisma rectangular, cuyas caras laterales y la base inferior
se cubren con cartón o madera. Para construir la estructura de la cocina,
utilizarán 4 listones de madera de 2,5 cm de ancho × 2,5 cm de alto × 2 m de
largo: dos listones para construir el perímetro de las bases, un listón para construir
el perímetro de la tapa y otro listón para las aristas que unirán las bases.
Considerado el material que disponen, ellos se plantean las siguientes
preguntas:
¿Qué
dimensiones tendrán las bases de la cocina para que su área sea la mayor
posible?
¿Qué
dimensiones tendrá la cocina solar?
Identificamos datos y relaciones
Respondemos
las siguientes preguntas para identificar los datos y relaciones presentes en la
situación:
¿Qué
datos identificamos en la situación problemática?
___________________________________
¿De
qué manera se relacionan estos datos?
___________________________________
¿De
qué manera podemos representar las dimensiones de las bases de la cocina?
___________________________________
¿Qué
es una función cuadrática?
___________________________________
Hacemos suposiciones o experimentos
Respondemos las siguientes preguntas y completamos la información que se
nos solicita:
¿Qué
medidas pueden tener los lados de la base de la cocina?
¿Qué
relación podemos establecer entre las medidas de los lados y el área de la base?
Si
el ancho midiera 10 cm, ¿cuánto mide el largo? _________ ¿y cuál sería el área?
Si
el ancho midiera 20 cm. ¿Cuánto mediría el largo? _________ ¿y cuál sería el
área?
Para organizar los valores, completamos la siguiente tabla:
|
Ancho (x) |
10 |
20 |
30 |
… |
… |
… |
… |
|
Largo (y) |
|
|
|
… |
… |
… |
… |
|
Área del rectángulo |
900 cm2 |
|
|
… |
… |
… |
… |
Luego, reflexionamos a partir de las siguientes preguntas:
¿Qué
relaciones podemos establecer entre la medida de los lados y el área?
¿Cómo
podemos determinar la mayor área de las bases de nuestra cocina? Justificamos
nuestra respuesta.
¿De
qué manera podemos organizar los datos?
Formulamos matemáticamente
Nos apoyamos en las siguientes preguntas para realizar nuestra
formulación:
¿Cómo
podemos determinar el área de forma directa?
____________________________________
Si
asignamos una variable a la longitud del ancho y otra a la del largo, ¿cómo expresaríamos
la longitud del largo en función de la medida del ancho?
____________________________________
¿Cómo
podemos expresar el área de la base?
____________________________________________________________________________
¿Cómo
se denomina a la expresión algebraica que hemos obtenido? Justificamos.
____________________________________________________________________________
Validamos nuestra solución
Completamos
la siguiente tabla. Para ello, escribimos el modelo matemático que hemos
obtenido en función del ancho de la base de la cocina y verificamos
si
los resultados que hemos obtenido en la tabla anterior se cumplen.
|
Ancho (x) |
10 |
20 |
… |
… |
… |
… |
|
|
−102 + 100 × 10 |
−202 + 100 × 20 |
… |
… |
… |
… |
|
|
−100 + 1000 = 900 |
−400 + 2000 = 1600 |
… |
… |
… |
… |
Comunicamos nuestra comprensión sobre la función
cuadrática
A partir de los resultados obtenidos, respondemos las siguientes
preguntas:
¿La
función cuadrática que se ha obtenido se puede representar gráficamente?
____________________________________________
¿Qué
forma tiene la gráfica de una función cuadrática?
____________________________________________
¿Cómo
se llama la gráfica de la función cuadrática?
____________________________________________
¿Cómo
interpretamos la gráfica de la función cuadrática en relación con las
dimensiones de las bases de la cocina?
____________________________________________
¿De
qué otra forma podemos expresar la función cuadrática? Justificamos nuestra
respuesta.
____________________________________________
Afianzamos nuestros aprendizajes
Utilizamos
GeoGebra para representar gráficamente la función cuadrática. Para ello, usamos
el modelo obtenido y generamos la gráfica con ayuda del aplicativo. Luego, interpretamos
dicha gráfica y respondemos las siguientes preguntas:
¿Cuál
es la variación del área cuando se incrementa la longitud de los lados de las bases?
________________________________________________________________________________________
¿En
qué punto de la gráfica se obtiene la mayor área?
________________________________________________________________________________________
Elaboramos afirmaciones a partir de las siguientes preguntas:
¿Cómo
nos ayuda la función cuadrática para determinar los lados de las bases de la
cocina de modo que tenga la mayor área posible? Justificamos nuestra respuesta.
________________________________________________________________________________________
¿Qué
medidas deben tener los lados de las bases de la cocina para que tenga la mayor
área posible? Justificamos nuestra respuesta.
________________________________________________________________________________________
Con
la cantidad de listones que se dispone y las medidas de los lados de las bases
que hemos obtenido, ¿qué dimensiones tendrá la cocina?
________________________________________________________________________________________
Reflexionamos sobre nuestro aprendizaje
Es momento de reflexionar sobre lo aprendido. Estas preguntas nos
ayudarán:
¿Qué
procedimientos nos ayudaron a responder las preguntas?
¿Qué
tomamos en cuenta para calcular el área de las bases de la cocina? Explicamos
el proceso realizado.
¿Cómo
nos ayuda el aplicativo GeoGebra en la elaboración de la gráfica de una función
cuadrática?
¿Por
qué será importante reducir el uso de combustibles contaminantes?
¿Qué
otras propuestas innovadoras podemos plantear?
Autoevaluación
|
Criterios de evaluación |
Lo logré |
Estoy en proceso de lograrlo
|
¿Qué puedo hacer para mejorar mis aprendizajes? |
|
Establezco
relaciones entre datos, valores desconocidos y variación entre magnitudes y
las transformo a funciones cuadráticas con coeficiente entero. |
|
|
|
|
Evalúo
si la expresión algebraica o gráfica que planteé representa las condiciones
del problema. |
|
|
|
|
Expreso
con representaciones gráficas, tabulares y simbólicas, y con lenguaje algebraico,
mi comprensión sobre la función cuadrática y sus valores máximos, para interpretar
mi solución en el contexto de la situación. |
|
|
|
|
Selecciono
las estrategias heurísticas, los métodos gráficos, los recursos y procedimientos
matemáticos más convenientes para solucionar ecuaciones cuadráticas, según las
condiciones del problema. |
|
|
|
|
Planteo
afirmaciones sobre las relaciones de cambio que observo entre las variables
de una función cuadrática. |
|
|
|


إرسال تعليق
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.