Taller de Arquitectura: Proyecciones Ortogonales
Sean los siguientes volúmenes:
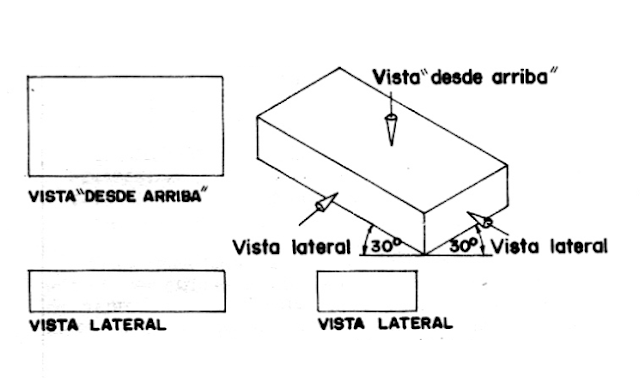
Estos volúmenes, como cualquier objeto, pueden ser representados bidimensionalmente (es decir, con dibujos en dos dimensiones o "planos"), a partir, al menos, de tres vistas que son las que se ven en una isometría, es decir: una vista desde un plano horizontal (desde arriba o desde abajo), y dos laterales, de la siguiente manera:
Para cada objeto, estas vistas son en realidad las proyecciones de dicho objeto sobre tres planos perpendiculares entre sí a los que llamaremos Plano Horizontal (H), Plano Frontal (F), y Plano de Perfil (P). Imaginemos una caja de cristal en la cual se encuentra un objeto dado, (con sus caras predominantes paralelas a los planos de la caja) y dibujemos en cada uno de los planos de proyección H, F y P (Horizontal, Frontal y de Perfil), la vista desde cada uno de ellos se tiene del objeto: tendremos las proyecciones ortográficas del volumen.
Proyecciones Ortofráficas
Podemos definir la proyección ortográfica como el método de representación gráfica exacta de un objeto a partir de las vistas que se obtienen trazando las proyecciones perpendiculares desde el objeto hacia los planos de proyección, perpendiculares entre sí.
Cada una de las vistas nos proporciona sólo información de dos dimensiones del objeto. Así, en plano horizontal vemos el ancho y la profundidad pero no la altura; en el plano frontal vemos el ancho y la altura, pero no la profundidad, y en el plano de perfil vemos la altura y la profundidad, pero no el ancho. Las tres vistas se complementan entre sí.
En algunos casos, dos vistas de un objeto podrían ser iguales, y si bien éste queda definido a partir de las dos vistas diferentes, es conveniente realizar las tres vistas, a fin de evitar errores de interpretación.
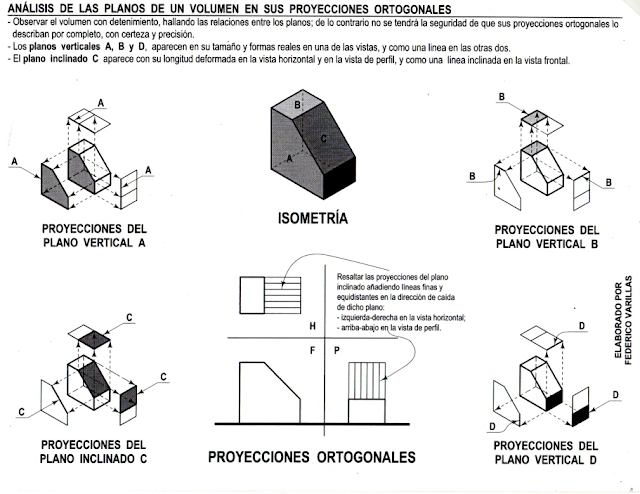
Ejemplo de volúmenes isométricos y sus proyecciones
Practicamos
Practica las siguientes proyecciones ortográficas descargando la lámina (Descargar)










إرسال تعليق
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.